Conditional average treatment effect estimation • ptLasso

require(glmnet)
#> Loading required package: glmnet
#> Loading required package: Matrix
#> Loaded glmnet 4.1-8

Background: CATE estimation and pretraining

In causal inference, we are often interested in predicting the treatment effect for individual observations; this is called the conditional average treatment effect (CATE). For example, before prescribing a drug to a patient, we want to know whether the drug is likely to work well for that patient - not just whether it works well on average. One tool to model the CATE is the R-learner (Nie and Wager (2021)), which minimizes the R loss:

$$ \hat{L}_n\{\tau(\cdot)\}=\arg \min_\tau \frac{1}{n}\sum\Bigl[ (y_i- m^*(x_i)) - (W_i-e^*(x_i))\tau(x_i) \Bigr]^2. $$ Here, $x_i$ and $y_i$ are the covariates and outcome for observation $i$ , $e^*(x_i)$ is the treatment propensity and $W_i$ the treatment assignment, and $m^*(x_i)$ is the conditional mean outcome ( $E[y_i \mid x = x_i]$ ). Then, $\hat\tau$ is the estimate of the heterogeneous treatment effect function.

This is fitted in stages: first, the R-learner fits $m^*$ and $e^*$ to get $\hat{m}^*$ and $\hat{e}^*$ ; then plugs in $\hat{m}^*(x_i)$ and $\hat{e}^*(x_i)$ to fit $\tau$ . A minor detail is that cross-fitting (or prevalidation) is used in the first stage so that the plugin value for e.g. $\hat{m}^*(x_i)$ comes from a model trained without using $x_i$ .

When $\tau$ is a linear function, then the second stage of fitting is straightforward. The values $\hat{m}^*(x_i)$ and $\hat{e}^*(x_i)$ are known, and we can use linear regression to model $y_i - \hat{m}^*(x_i)$ as a function of the weighted feature vector $(W_i-\hat{e}^*(x_i)) x_i$ . This is what we will do in the following example.

How can pretraining be useful here? Well, we are separately fitting models for $m^*$ (the conditional mean) and $\tau$ (the heterogeneous treatment effect), and these two functions are likely to share support: it is sensible to assume that the features that modulate the mean treatment effect also modulate the heterogeneous treatment effect. We can use pretraining by (1) training a model for $m^*$ and (2) using the support from this model to guide the fitting of $\tau$ . Note that the offset is not used in this case; $m^*$ and $\tau$ are designed to predict different outcomes.

A simulated example

Here is an example. We will simplify the problem by assuming treatment has been randomized – the true $e^*(x_i) = 0.5$ for all $i$ .

set.seed(1234)

n = 600; ntrain = 300
p = 20
     
x = matrix(rnorm(n*p), n, p)

# Treatment assignment
w = rbinom(n, 1, 0.5)

# m^*
m.coefs = c(rep(2,10), rep(0, p-10))
m = x %*% m.coefs

# tau
tau.coefs = runif(p, 0.5, 1)*m.coefs 
tau = 1.5*m + x%*%tau.coefs

mu = m + w * tau
y  = mu + 10 * rnorm(n)
cat("Signal to noise ratio:", var(mu)/var(y-mu))
#> Signal to noise ratio: 2.301315

# Split into train/test
xtest = x[-(1:ntrain), ]
tautest = tau[-(1:ntrain)] 
wtest = w[-(1:ntrain)]

x = x[1:ntrain, ]
y = y[1:ntrain] 
w = w[1:ntrain]

# Define training folds
nfolds = 10
foldid = sample(rep(1:10, trunc(nrow(x)/nfolds)+1))[1:nrow(x)]

We begin model fitting, starting with our estimate of $e^*$ (the probability of receiving the treatment). To fit $\tau$ , we will also need to record the cross-fitted $\hat{e}^*(x)$ .


e_fit = cv.glmnet(x, w, foldid = foldid,
                  family="binomial", type.measure="deviance",
                  keep = TRUE)

e_hat = e_fit$fit.preval[, e_fit$lambda == e_fit$lambda.1se]
e_hat = 1/(1 + exp(-e_hat))

Now, stage 1 of pretraining: fit a model for $m^*$ and record the support. As before, we also record the cross-fitted $\hat{m}^*(x)$ .


m_fit = cv.glmnet(x, y, foldid = foldid, keep = TRUE)

m_hat = m_fit$fit.preval[, m_fit$lambda == m_fit$lambda.1se]

bhat = coef(m_fit, s = m_fit$lambda.1se)
support = which(bhat[-1] != 0)

To fit $\tau$ , we will regress $\tilde{y} = y_i - \hat{m}^*(x_i)$ on $\tilde{x} = (w_i - \hat{e}^*(x_i)) x_i$ ; we’ll define them here:

y_tilde = y - m_hat
x_tilde = cbind(as.numeric(w - e_hat) * cbind(1, x))

And now, pretraining for $\tau$ . Loop over $\alpha = 0, 0.1, \dots, 1$ ; for each $\alpha$ , fit a model for $\tau$ using the penalty factor defined by the support of $\hat{m}$ and $\alpha$ . We’ll keep track of our CV MSE at each step so that we can choose the $\alpha$ that minimizes the MSE.

cv.error = NULL
alphalist = seq(0, 1, length.out = 11)

for(alpha in alphalist){
  pf = rep(1/alpha, p)
  pf[support] = 1
  pf = c(0, pf) # Don't penalize the intercept
  
  tau_fit = cv.glmnet(x_tilde, y_tilde, 
                      foldid = foldid,
                      penalty.factor = pf,
                      intercept = FALSE, # already include in x_tilde
                      standardize = FALSE)
  cv.error = c(cv.error, min(tau_fit$cvm))
}


plot(alphalist, cv.error, type = "b",
     xlab = expression(alpha), 
     ylab = "CV MSE", 
     main = bquote("CV mean squared error as a function of " ~ alpha))
abline(v = alphalist[which.min(cv.error)])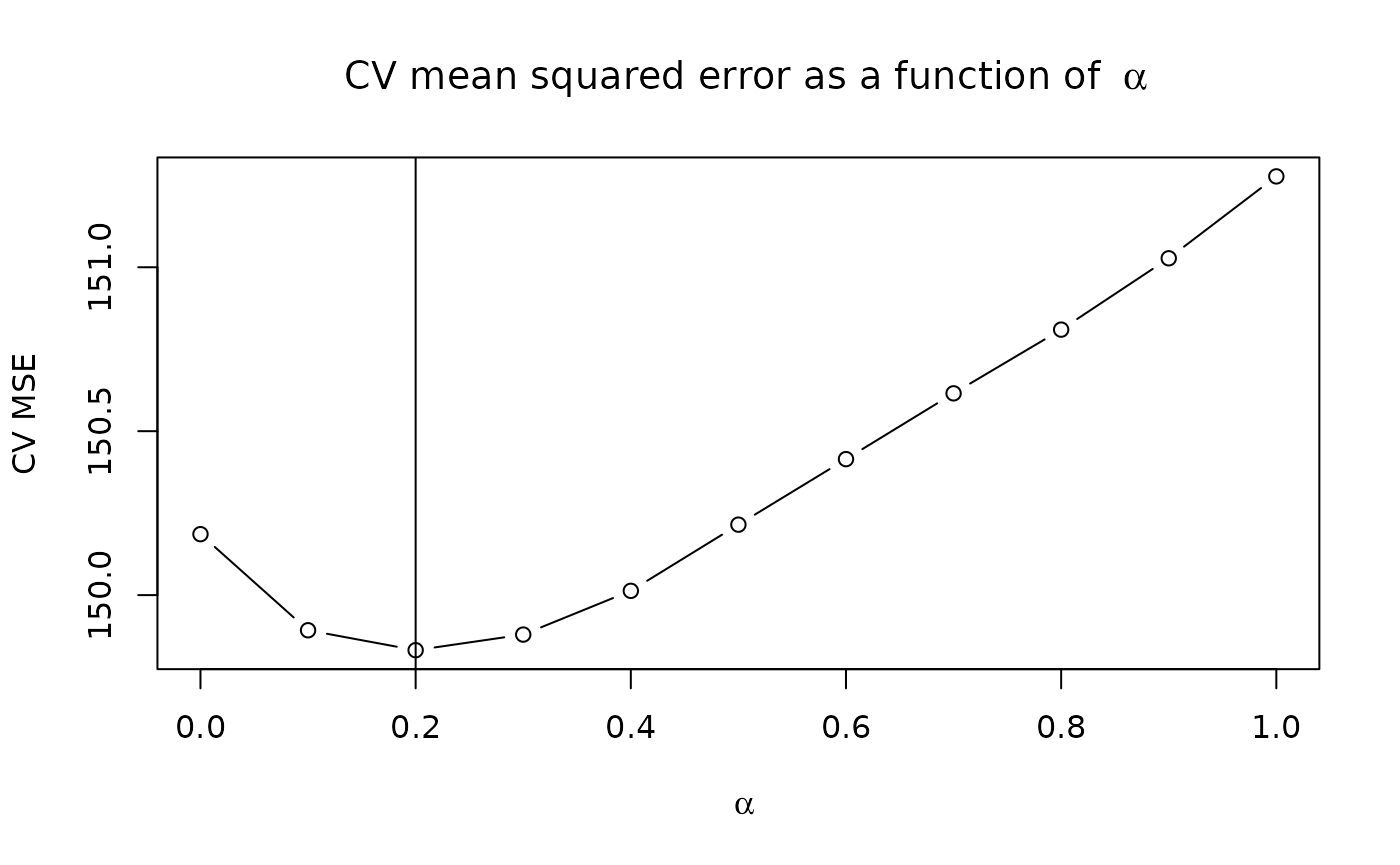

In the plot above, the value at $\alpha = 1$ corresponds to the usual R learner, which makes no assumption about a shared support between $\tau$ and $m^*$ . Based on the plot, we choose $\alpha = 0.2$ as our best performing model:


best.alpha = alphalist[which.min(cv.error)]
cat("Chosen alpha:", best.alpha)
#> Chosen alpha: 0.2

pf = rep(1/best.alpha, p)
pf[support] = 1
pf = c(0, pf)
tau_fit = cv.glmnet(x_tilde, y_tilde, foldid = foldid,
                    penalty.factor = pf,
                    intercept = FALSE,
                    standardize = FALSE)

To concretely compare the pretrained R-learner with the usual R-learner, we’ll train the usual R-learner here:

tau_rlearner = cv.glmnet(x_tilde, y_tilde, foldid = foldid, 
                         penalty.factor = c(0, rep(1, ncol(x))),
                         intercept = FALSE,
                         standardize = FALSE)

As anticipated, pretraining improves the prediction squared error relative to the R learner – this is how we designed our simulation:


rlearner_preds   = predict(tau_rlearner, cbind(1, xtest), s = "lambda.min")
cat("R-learner PSE: ", 
    round(mean((rlearner_preds - tautest)^2), 2))
#> R-learner PSE:  45.85

pretrained_preds = predict(tau_fit, cbind(1, xtest), s = "lambda.min")
cat("Pretrained R-learner PSE: ", 
    round(mean((pretrained_preds - tautest)^2), 2))
#> Pretrained R-learner PSE:  37.63

What if the pretraining assumption is wrong?

Here, we repeat everything from above, only now there is no overlap in the support of $m^*$ and $\tau$ .

######################################################
# Simulate data
######################################################
x = matrix(rnorm(n*p), n, p)

# Treatment assignment
w = rbinom(n, 1, 0.5)

# m^*
m.coefs = c(rep(2,10), rep(0, p-10))
m = x %*% m.coefs

# tau
# Note these coefficients have no overlap with m.coefs!
tau.coefs = c(rep(0, 10), rep(2, 10), rep(0, p-20))
tau = x%*%tau.coefs

mu = m + w * tau
y  = mu + 10 * rnorm(n)
cat("Signal to noise ratio:", var(mu)/var(y-mu))
#> Signal to noise ratio: 0.6938152

# Split into train/test
xtest = x[-(1:ntrain), ]
tautest = tau[-(1:ntrain)] 
wtest = w[-(1:ntrain)]

x = x[1:ntrain, ]
y = y[1:ntrain] 
w = w[1:ntrain]

######################################################
# Model fitting: e^*
######################################################
e_fit = cv.glmnet(x, w, foldid = foldid,
                  family="binomial", type.measure="deviance",
                  keep = TRUE)
e_hat = e_fit$fit.preval[, e_fit$lambda == e_fit$lambda.1se]
e_hat = 1/(1 + exp(-e_hat))

######################################################
# Model fitting: m^*
######################################################
m_fit = cv.glmnet(x, y, foldid = foldid, keep = TRUE)

m_hat = m_fit$fit.preval[, m_fit$lambda == m_fit$lambda.1se]

bhat = coef(m_fit, s = m_fit$lambda.1se)
support = which(bhat[-1] != 0)

######################################################
# Pretraining: tau
######################################################
y_tilde = y - m_hat
x_tilde = cbind(as.numeric(w - e_hat) * cbind(1, x))

cv.error = NULL
alphalist = seq(0, 1, length.out = 11)

for(alpha in alphalist){
  pf = rep(1/alpha, p)
  pf[support] = 1
  pf = c(0, pf) # Don't penalize the intercept
  
  tau_fit = cv.glmnet(x_tilde, y_tilde, 
                      foldid = foldid,
                      penalty.factor = pf,
                      intercept = FALSE, # already include in x_tilde
                      standardize = FALSE)
  cv.error = c(cv.error, min(tau_fit$cvm))
}

# Our final model for tau:
best.alpha = alphalist[which.min(cv.error)]
cat("Chosen alpha:", best.alpha)
#> Chosen alpha: 1

pf = rep(1/best.alpha, p)
pf[support] = 1
pf = c(0, pf)
tau_fit = cv.glmnet(x_tilde, y_tilde, foldid = foldid,
                    penalty.factor = pf,
                    intercept = FALSE,
                    standardize = FALSE)

######################################################
# Fit the usual R-learner:
######################################################
tau_rlearner = cv.glmnet(x_tilde, y_tilde, foldid = foldid, 
                         penalty.factor = c(0, rep(1, ncol(x))),
                         intercept = FALSE,
                         standardize = FALSE)

######################################################
# Measure performance:
######################################################
rlearner_preds = predict(tau_rlearner, cbind(1, xtest), s = "lambda.min")
cat("R-learner prediction squared error: ", 
    round(mean((rlearner_preds - tautest)^2), 2))
#> R-learner prediction squared error:  31.11

pretrained_preds = predict(tau_fit, cbind(1, xtest), s = "lambda.min")
cat("Pretrained R-learner prediction squared error: ", 
    round(mean((pretrained_preds - tautest)^2), 2))
#> Pretrained R-learner prediction squared error:  31.11

Pretraining has not hurt our performance, even though the support of $m^*$ and $\tau$ are not shared. Why? Recall that we defined $y = m^*(x) + W * \tau(x) + \epsilon$ , so the relationship between $y$ and $x$ is a function of the supports of both $m^*$ and $\tau$ . In the first stage of pretraining, we fitted $m^*$ using y ~ x – so the support of $m^*$ should include the support of $\tau$ . As a result, using pretraining with the R-learner should not harm predictive performance.

Nie, Xinkun, and Stefan Wager. 2021. “Quasi-Oracle Estimation of Heterogeneous Treatment Effects.” Biometrika 108 (2): 299–319.