Unsupervised pretraining • ptLasso

require(glmnet)
#> Loading required package: glmnet
#> Loading required package: Matrix
#> Loaded glmnet 4.1-8

Suppose we have a dataset with features $X$ and response $y$ . Suppose we also have a large set of unlabeled data $X^*$ . Here, we show how to pretrain a model using $X^*$ . The steps are:

Do sparse PCA using $X^*$ . Identify the nonzero features in the first principal component (PC).
Use glmnet (or cv.glmnet) to train model using $X$ and $y$ . Define the penalty factor using the support identified by sparse PCA. Unlike the usual pretraining, there is no offset defined by sparse PCA.

In step 1, we may choose to use the nonzero features from the first $k$ PCs instead of just the first PC; in the examples that follow, we use only the first PC for simplicity.

We will demonstrate unsupervised pretraining using simulated data. The covariates $X$ and $X^*$ are drawn from a multivariate normal distribution where the first 10 features describe most of the variance, and $y$ is defined as $X \beta + \epsilon$ , where only the first 10 coefficients in $\beta$ are nonzero and $\epsilon$ is noise. In this example, we have 10 times as much unlabeled data as labeled data; this generally happens when labels are difficult to obtain.

require(MASS) # for mvrnorm
#> Loading required package: MASS

set.seed(1234)

n = 100; p = 150; 

mu = rep(0, p)
sigma <- matrix(runif(p^2)*2-1, ncol=p) 
sigma[, 11:p] = 1e-2 # The first 10 features are the most important
sigma <- t(sigma) %*% sigma
diag(sigma)[11:p] = 1

x     = mvrnorm(n = n, mu = mu, Sigma = sigma)
xtest = mvrnorm(n = n, mu = mu, Sigma = sigma)
xstar = mvrnorm(n = 10 * n, mu = mu, Sigma = sigma) # unlabeled

noise = 3
beta = c(rep(1, 10), rep(0, p - 10))
y     = x %*% beta     + noise * rnorm(n)
ytest = xtest %*% beta + noise * rnorm(n)

train.folds = sample(rep(1:10, 10))

Now, we do sparse PCA using $X^*$ and we identify the features with nonzero loadings in the first PC. The argument $k = 1$ means that we only obtain the first PC.

require(sparsepca)
#> Loading required package: sparsepca

pcs = spca(xstar, k = 1, verbose=FALSE, alpha=1e-2, beta=1e-2)
nonzero.loadings = which(pcs$loadings != 0)

We set ourselves up for success: because of how we simulated our data, we know that the first 10 features are those that explain the variance in $X$ . These are also the features that define the relationship between $X$ and $y$ . Let’s check that sparse PCA has found the right features:

nonzero.loadings
#>  [1]  1  2  3  4  5  6  7  8  9 10

Now, we are ready to model! We don’t need to call ptLasso here. All we need to do is call cv.glmnet across a grid of values of $\alpha$ with a different penalty.factor for each call. Note that offset is not used – sparse PCA identifies which features may important, but it doesn’t suggest a value for the fitted coefficients.

To do model selection, we want to know which value of $\alpha$ gave us the best CV error. Fortunately, cv.glmnet will record the CV MSE for each model in a vector called cvm; we just need to keep track of the minimum error from each model.


alphalist = seq(0, 1, length.out = 11)

cvm = NULL
for(alpha in alphalist){
  # Define the penalty factor:
  pf = rep(1/alpha, p)
  pf[nonzero.loadings] = 1
  
  # Train a model:
  model = cv.glmnet(x, y, family = "gaussian", type.measure = "mse",
                              penalty.factor = pf, 
                              foldid = train.folds)
  
  # Record the minmum CV MSE for this model:
  cvm = c(cvm, min(model$cvm))
}

best.alpha = alphalist[which.min(cvm)]

# Plot performance as a function of alpha
# with a vertical line to show us the minimum mse:
plot(alphalist, cvm, 
     xlab = expression(alpha), 
     ylab = "Mean squared error (CV)"
)
abline(v = best.alpha)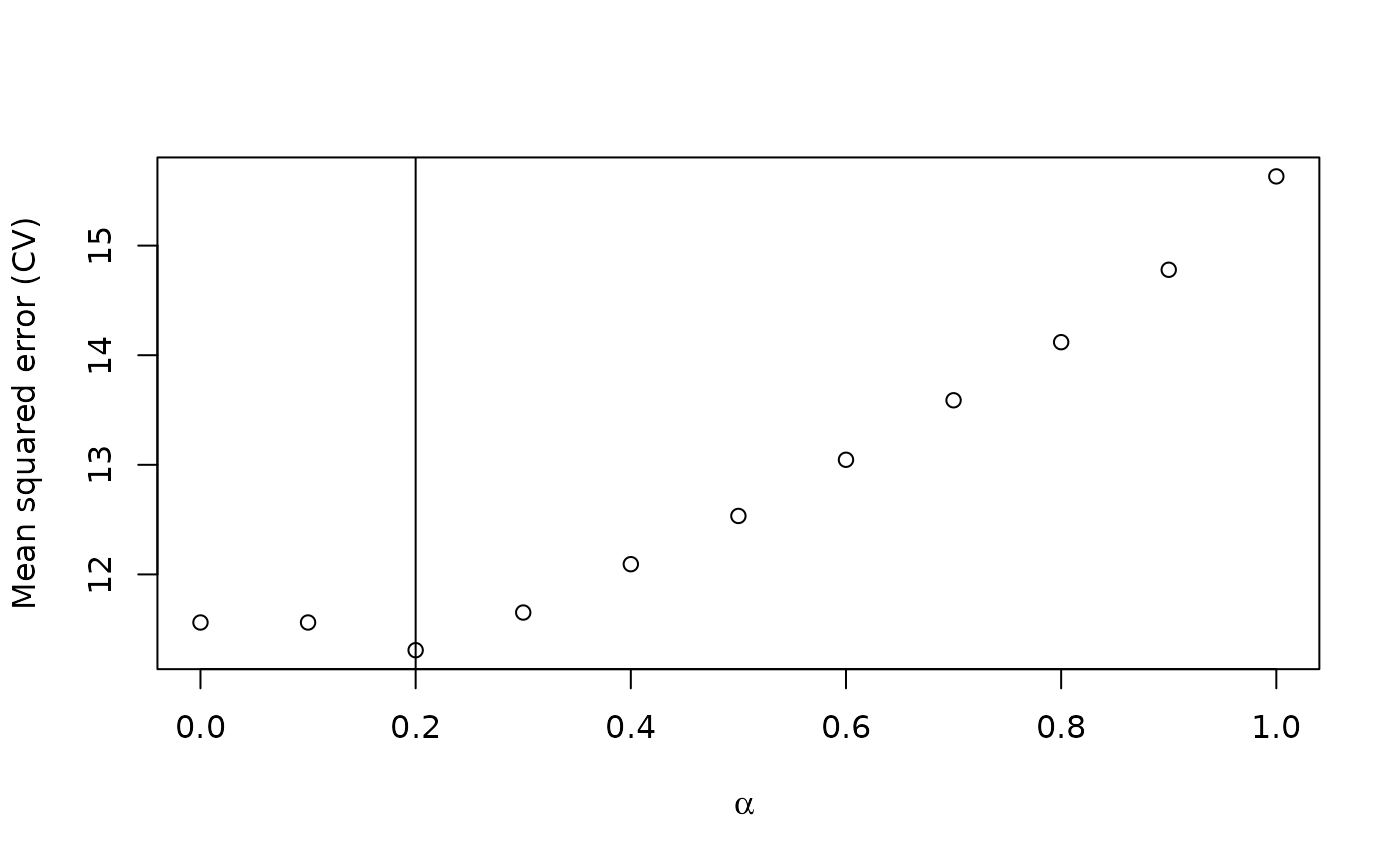

So, using CV performance as a metric, we choose $\alpha = 0.2$ . Now, we train our final model and predict and measure performance with our held-out data. We find that pretraining gives us a boost in performance.

pf = rep(1/best.alpha, p)
pf[nonzero.loadings] = 1

selected.model =  cv.glmnet(x, y, family = "gaussian", type.measure = "mse",
                              penalty.factor = pf, 
                              foldid = train.folds)

# Prediction squared error with pretraining:
assess.glmnet(selected.model, xtest, newy = ytest, s = "lambda.min")["mse"]
#> $mse
#> lambda.min 
#>   9.914999 
#> attr(,"measure")
#> [1] "Mean-Squared Error"

without.pretraining =  cv.glmnet(x, y, family = "gaussian", type.measure = "mse",
                                 foldid = train.folds)

# Prediction squared error without pretraining:
assess.glmnet(without.pretraining, xtest, newy = ytest, s = "lambda.min")["mse"]
#> $mse
#> lambda.min 
#>   14.42903 
#> attr(,"measure")
#> [1] "Mean-Squared Error"