Multi-response data with mixed response types • ptLasso

require(glmnet)
#> Loading required package: glmnet
#> Loading required package: Matrix
#> Loaded glmnet 4.1-8
require(survival)
#> Loading required package: survival

Muti-response data consists of datasets with covariates $X$ and multiple outcomes $y_1, y_2, y_3, \dots$ . If these outcomes are all continuous, then it may be natural to treat this as a multitask learning problem (see the section “Multi-response data with Gaussian responses”). If the outcomes have mixed types however – e.g. $y_1$ is continuous, $y_2$ binary and $y_3$ survival – then the problem is slightly more challenging, because there are fewer methods developed for this setting.

Pretraining is a natural fit for this task: we often believe that there is shared information between $y_1$ , $y_2$ and $y_3$ . If we fit 3 separate models, we never get to take advantage of any shared information; further, because the outcomes have different types, there are very few methods to fit one model for all outcomes (an “overall model”).

So, we will use pretraining to pass information between models. We will:

fit a model for $y_1$ ,
extract the offset and support from this model,
use the offset and support (the usual pretraining) to train models for $y_2$ and $y_3$ .

There is one small detail here: we must choose the primary outcome $y_1$ . This is an important choice because it will form the support and offset for the other two outcomes. We recommend making this selection using domain knowledge, but cross-validation (or a validation set) can of course be used.

Here, we walk through an example with simulated data with three outcomes $y_1, y_2$ and $y_3$ . The three outcomes have overlapping support; the first 10 features are predictive . Outcomes 2 and 3 additionally have 5 features unique to each of them. We’ll define $y_1$ to be continuous, $y_2$ to be binomial and $y_3$ to be survival.

set.seed(1234)

# Define constants
n = 600          # Total number of samples
ntrain = 300     # Number of training samples
p = 50           # Number of features

# Define covariates     
x = matrix(rnorm(n*p), n, p)

# y1: continuous response
beta1 = c(rep(.5, 10), rep(0, p-10))
y1 = x %*% beta1 + rnorm(n)

# y2: binomial response
beta2 = runif(p, min = 0.5, max = 1) * beta1  # Shared with group 1
beta2 = beta2 + c(rep(0, 10), 
                  runif(5, min = 0, max = 0.5), 
                  rep(0, p-15)) # Individual
y2 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta2)))

# y3: survival response
beta3 = beta1  # Shared with group 1
beta3 = beta3 + c(rep(0, 10), 
                  runif(5, min = -0.1, max = 0.1),
                  rep(0, p-15)) # Individual
y3.true = - log(runif(n)) / exp(x %*% beta3)
y3.cens = runif(n)
y3 = Surv(pmin(y3.true, y3.cens), y3.true <= y3.cens)

# Split into train and test
xtest = x[-(1:ntrain), ]
y1test = y1[-(1:ntrain)]
y2test = y2[-(1:ntrain)]
y3test = y3[-(1:ntrain), ]

x = x[1:ntrain, ]
y1 = y1[1:ntrain]
y2 = y2[1:ntrain]
y3 = y3[1:ntrain, ]

# Define training folds
nfolds = 10
foldid = sample(rep(1:10, trunc(nrow(x)/nfolds)+1))[1:nrow(x)]

For the first step of pretraining, train a model for the primary outcome ( $y_1$ ) and record the offset and support – these will be used when training the models for $y_2$ and $y_3$ .

y1_fit = cv.glmnet(x, y1, keep=TRUE, foldid = foldid)

train_offset = y1_fit$fit.preval[, y1_fit$lambda == y1_fit$lambda.1se]
support = which(coef(y1_fit, s = y1_fit$lambda.1se)[-1] != 0)

Now we have everything we need to train the models for $y_2$ and $y_3$ . In the following code, we loop over $\alpha = 0, 0.1, \dots, 1$ ; in each step, we (1) train models for $y_2$ and $y_3$ and (2) record the CV error from both models. The CV error will be used to determine values of $\alpha$ to use for the final models.

cv.error.y2 = cv.error.y3 = NULL
alphalist = seq(0, 1, length.out = 11)

for(alpha in alphalist){
  pf = rep(1/alpha, p)
  pf[support] = 1
  
  offset = (1 - alpha) * train_offset
    
  y2_fit = cv.glmnet(x, y2, 
                     foldid = foldid,
                     offset = offset,
                     penalty.factor = pf,
                     family = "binomial",
                     type.measure = "auc")
  cv.error.y2 = c(cv.error.y2, max(y2_fit$cvm))
  
  y3_fit = cv.glmnet(x, y3, 
                     foldid = foldid,
                     offset = offset,
                     penalty.factor = pf,
                     family = "cox",
                     type.measure = "C")
  cv.error.y3 = c(cv.error.y3, max(y3_fit$cvm))
}

Plotting our CV performance suggests the value of $\alpha$ we should choose for each outcome:

par(mfrow = c(2, 1))
plot(alphalist, cv.error.y2, type = "b",
     main = bquote("Outcome 2: CV AUC vs " ~ alpha),
     xlab = expression(alpha),
     ylab = "CV AUC")
abline(v = alphalist[which.max(cv.error.y2)])

plot(alphalist, cv.error.y3, type = "b",
     main = bquote("Outcome 3: CV C index vs " ~ alpha),
     xlab = expression(alpha),
     ylab = "CV C index")
abline(v = alphalist[which.max(cv.error.y3)])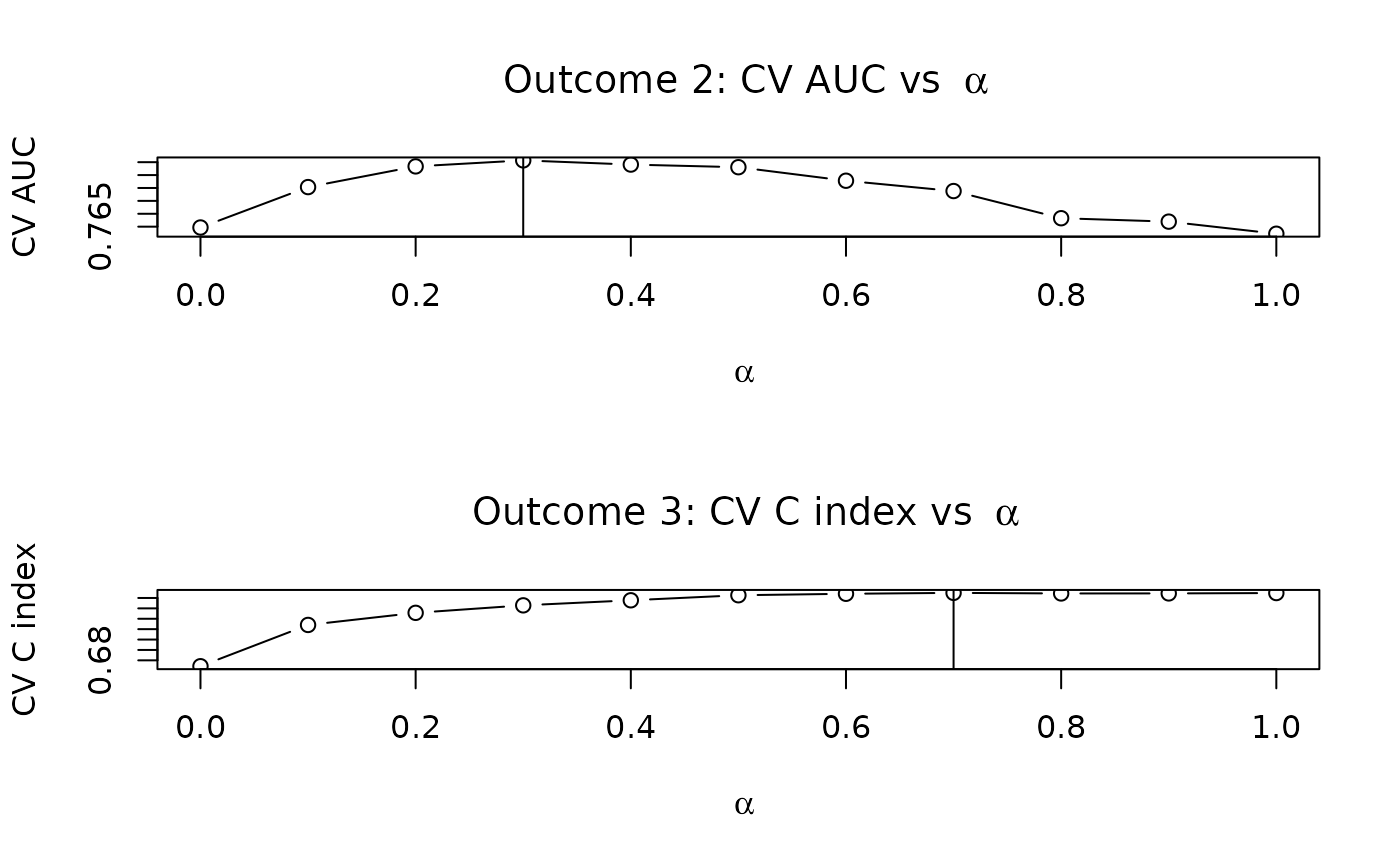

Now that we have selected our values of $\alpha$ , we can fit the final models for $y_2$ and $y_3$ :

############################################################
# Model for y2:
############################################################
best.alpha.y2 = alphalist[which.max(cv.error.y2)]
pf = rep(1/best.alpha.y2, p); pf[support] = 1

y2_fit = cv.glmnet(x, y2, 
                   foldid = foldid,
                   offset = (1-best.alpha.y2) * train_offset,
                   penalty.factor = pf,
                   family = "binomial",
                   type.measure = "auc")

############################################################
# Repeat for y3:
############################################################
best.alpha.y3 = alphalist[which.max(cv.error.y3)]
pf = rep(1/best.alpha.y3, p); pf[support] = 1

y3_fit = cv.glmnet(x, y3, 
                   foldid = foldid,
                   offset = (1-best.alpha.y3) * train_offset,
                   penalty.factor = pf,
                   family = "cox", 
                   type.measure = "C")

We will also train models for $y_2$ and $y_3$ without pretraining; this is a natural benchmark.

y2_fit_no_pretrain = cv.glmnet(x, y2, foldid = foldid, 
                               family = "binomial", type.measure = "auc")

y3_fit_no_pretrain = cv.glmnet(x, y3, 
                               foldid = foldid, 
                               family = "cox", type.measure = "C")

All of our models have been trained. Let’s compare performance with and without pretraining; we’ll start with the model for $y_2$ .

testoffset = predict(y1_fit, xtest, s = "lambda.1se")

cat("Model 2 AUC with pretraining:", 
    round(assess.glmnet(y2_fit, xtest, newy = y2test, 
                        newoffset = (1 - best.alpha.y2) * testoffset)$auc, 2),
    fill=TRUE)
#> Model 2 AUC with pretraining: 0.76

cat("Model 2 AUC without pretraining:", 
    round(assess.glmnet(y2_fit_no_pretrain, xtest, newy = y2test)$auc, 2)
    )
#> Model 2 AUC without pretraining: 0.66

And now, the models for $y_3$ :

cat("Model 3 C-index with pretraining:", 
    round(assess.glmnet(y3_fit, xtest, newy = y3test, 
                        newoffset = (1 - best.alpha.y3) * testoffset)$C, 2))
#> Model 3 C-index with pretraining: 0.8

cat("Model 3 C-index without pretraining:", 
    round(assess.glmnet(y3_fit_no_pretrain, xtest, newy = y3test)$C, 2)
    )
#> Model 3 C-index without pretraining: 0.78

For both $y_2$ and $y_3$ , we saw a performance improvement using pretraining. We didn’t technically need to train the individual (non-pretrained) models for $y_2$ and $y_3$ : during our CV loop to choose $\alpha$ , we saw the cross validation performance for the individual models (the special case when $\alpha = 1$ ), and CV recommended a smaller value of $\alpha$ for both outcomes.

Note that, in this example, we trained a model using $y_1$ , and then used this model to form the offset and support for the models for $y_2$ and $y_3$ in parallel. But using pretraining for multi-response data is flexible. Pretraining is simply a method to pass information from one model to another, and we are free to choose how information flows. For example, we chose to pass information from model 1 ( $y_1$ ) to model 2 ( $y_2$ ) and to model 3 ( $y_3$ ). But, we could have instead chained our models to pass information from model 1 to model 2, and then from model 2 to model 3 in the following way:

fit a model for $y_1$ ,
extract the offset and support from this model,
use the offset and support (the usual pretraining) to train a model for $y_2$ ,
extract the offset and support from this second model, and
use them to train a model for $y_3$ .

In this framework, the model for $y_3$ depends implicitly on both the models for $y_1$ and $y_2$ , as the offset and support for the model for $y_2$ were informed by the model for $y_1$ . Choosing how information should be passed between outcomes is context specific and we recommend relying on domain knowledge for selecting an approach (though many options may be tried and compared with cross-validation or a validation set).