Fits a pretrained lasso model using the glmnet package, for a fixed choice of the pretraining hyperparameter alpha. Additionally fits an "overall" model (using all data) and "individual" models (use each individual group). Can fit input-grouped data with Gaussian, multinomial, binomial or Cox outcomes, and target-grouped data, which necessarily has a multinomial outcome. Many ptLasso arguments are passed directly to glmnet, and therefore the glmnet documentation is another good reference for ptLasso.
Usage
ptLasso(
x,
y,
groups = NULL,
alpha = 0.5,
family = c("default", "gaussian", "multinomial", "binomial", "cox"),
type.measure = c("default", "mse", "mae", "auc", "deviance", "class", "C"),
use.case = c("inputGroups", "targetGroups", "multiresponse", "timeSeries"),
overall.lambda = c("lambda.1se", "lambda.min"),
overall.gamma = "gamma.1se",
foldid = NULL,
nfolds = 10,
standardize = TRUE,
verbose = FALSE,
weights = NULL,
penalty.factor = rep(1, p),
fitoverall = NULL,
fitind = NULL,
en.alpha = 1,
group.intercepts = TRUE,
...
)Arguments
- x
input matrix, of dimension nobs x nvars; each row is an observation vector. Can be in sparse matrix format (inherit from class '"sparseMatrix"' as in package 'Matrix'). Requirement: 'nvars >1'; in other words, 'x' should have 2 or more columns. If 'use.case = "timeSeries"', then x may be a list of matrices with identical dimensions, one for each point in time.
- y
response variable. Quantitative for 'family="gaussian"'. For 'family="binomial"' should be either a factor with two levels, or a two-column matrix of counts or proportions (the second column is treated as the target class; for a factor, the last level in alphabetical order is the target class). For 'family="multinomial"', can be a 'nc>=2' level factor, or a matrix with 'nc' columns of counts or proportions. For either '"binomial"' or '"multinomial"', if 'y' is presented as a vector, it will be coerced into a factor. For 'family="cox"', preferably a 'Surv' object from the survival package: see Detail section for more information. For 'use.case = "multiresponse"' or 'use.case = "timeSeries"', 'y' is a matrix of responses.
- groups
A vector of length nobs indicating to which group each observation belongs. Only for 'use.case = "inputGroups"'.
- alpha
The pretrained lasso hyperparameter, with \(0\le\alpha\le 1\). The range of alpha is from 0 (which fits the overall model with fine tuning) to 1 (the individual models). The default value is 0.5, chosen mostly at random. To choose the appropriate value for your data, please either run
ptLassowith a few choices of alpha and evaluate with a validation set, or use cv.ptLasso, which recommends a value of alpha using cross validation.- family
Either a character string representing one of the built-in families, or else a 'glm()' family object. For more information, see Details section below or the documentation for response type (see above).
- type.measure
loss to use for cross-validation within each individual, overall, or pretrained lasso model. Currently five options, not all available for all models. The default is 'type.measure="deviance"', which uses squared-error for gaussian models (a.k.a 'type.measure="mse"' there), deviance for logistic and poisson regression, and partial-likelihood for the Cox model. 'type.measure="class"' applies to binomial and multinomial logistic regression only, and gives misclassification error. 'type.measure="auc"' is for two-class logistic regression only, and gives area under the ROC curve. 'type.measure="mse"' or 'type.measure="mae"' (mean absolute error) can be used by all models except the '"cox"'; they measure the deviation from the fitted mean to the response. 'type.measure="C"' is Harrel's concordance measure, only available for 'cox' models.
- use.case
The type of grouping observed in the data. Can be one of "inputGroups", "targetGroups", "multiresponse" or "timeSeries".
- overall.lambda
The choice of lambda to be used by the overall model to define the offset and penalty factor for pretrained lasso. Defaults to "lambda.1se", could alternatively be "lambda.min". This choice of lambda will be used to compute the offset and penalty factor (1) during model training and (2) during prediction. In the predict function, another lambda must be specified for the individual models, the second stage of pretraining and the overall model.
- overall.gamma
For use only when the option
relax = TRUEis specified. The choice of gamma to be used by the overall model to define the offset and penalty factor for pretrained lasso. Defaults to "gamma.1se", but "gamma.min" is also a good option. This choice of gamma will be used to compute the offset and penalty factor (1) during model training and (2) during prediction. In the predict function, another gamma must be specified for the individual models, the second stage of pretraining and the overall model.- foldid
An optional vector of values between 1 and
nfoldsidentifying what fold each observation is in. If supplied,nfoldcan be missing.- nfolds
Number of folds for CV (default is 10). Although
nfoldscan be as large as the sample size (leave-one-out CV), it is not recommended for large datasets. Smallest value allowable isnfolds = 3.- standardize
Should the predictors be standardized before fitting (default is TRUE).
- verbose
If
verbose=TRUE, print a statement showing which model is currently being fit withcv.glmnet.- weights
observation weights. Default is 1 for each observation.
- penalty.factor
Separate penalty factors can be applied to each coefficient. This is a number that multiplies 'lambda' to allow differential shrinkage. Can be 0 for some variables, which implies no shrinkage, and that variable is always included in the model. Default is 1 for all variables (and implicitly infinity for variables listed in 'exclude'). For more information, see
?glmnet. For pretraining, the user-supplied penalty.factor will be multiplied by that computed by the overall model.- fitoverall
An optional cv.glmnet object specifying the overall model. This should have been trained on the full training data, with the argument 'keep = TRUE'.
- fitind
An optional list of cv.glmnet objects specifying the individual models. These should have been trained on the original training data, with the argument 'keep = TRUE'.
- en.alpha
The elasticnet mixing parameter, with 0 <= en.alpha <= 1. The penalty is defined as (1-alpha)/2||beta||_2^2+alpha||beta||_1. 'alpha=1' is the lasso penalty, and 'alpha=0' the ridge penalty. Default is `en.alpha = 1` (lasso).
- group.intercepts
For 'use.case = "inputGroups"' only. If `TRUE`, fit the overall model with a separate intercept for each group. If `FALSE`, ignore the grouping and fit one overall intercept. Default is `TRUE`.
- ...
Additional arguments to be passed to the cv.glmnet functions. Notable choices include
"trace.it"and"parallel". Iftrace.it = TRUE, then a progress bar is displayed for each call to"cv.glmnet"; useful for big models that take a long time to fit. Ifparallel = TRUE, use parallelforeachto fit each fold. Must register parallel before hand, such asdoMCor others. ptLasso does not support the argumentsintercept,offset,fitandcheck.args.
Value
An object of class "ptLasso", which is a list with the ingredients of the fitted models.
- call
The call that produced this object.
- k
The number of groups (for 'use.case = "inputGroups"').
- nresps
The number of responses (for 'use.case = "multiresponse"' and 'use.case = "timeseries"').
- alpha
The value of alpha used for pretraining.
- group.levels
IDs for all of the groups used in training (for 'use.case = "inputGroups"').
- group.legend
Mapping from user-supplied group ids to numeric group ids. For internal use (e.g. with predict). (For 'use.case = "inputGroups"')
- fitoverall
A fitted
cv.glmnetobject trained using the full data. Not available for 'use.case = "timeseries"'.- fitpre
A list of fitted (pretrained)
cv.glmnetobjects, one trained with each data group or response.- fitind
A list of fitted
cv.glmnetobjects, one trained with each group or response.- fitoverall.lambda
Lambda used with fitoverall, to compute the offset for pretraining.
- fitoverall.gamma
Gamma used with fitoverall when 'relax = TRUE', to compute the offset for pretraining.
References
Friedman, J., Hastie, T., & Tibshirani, R. (2010). Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software, 33(1), 1-22.
Examples
# Getting started. First, we simulate data: we need covariates x, response y and group IDs.
set.seed(1234)
n=100
p=10
n.groups=2
x = matrix(rnorm(n*p), n, p)
y = rnorm(n)
groups = sort(rep(1:n.groups, n/n.groups))
xtest = matrix(rnorm(n*p), n, p)
ytest = rnorm(n)
groupstest = sort(rep(1:n.groups, n/n.groups))
# Now, we can fit a ptLasso model:
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "gaussian",
nfolds = 3, type.measure = "mse")
plot(fit) # to see all of the cv.glmnet models trained
 predict(fit, xtest, groupstest) # to predict on new data
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest)
#>
#>
#>
#> alpha = 0.5
#>
#> Support size:
#>
#> Overall 1
#> Pretrain 1 (0 common + 1 individual)
#> Individual 1
predict(fit, xtest, groupstest, ytest=ytest) # if ytest is included, we also measure performance
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean group_1 group_2 r^2
#> Overall 1.162 1.162 1.423 0.9020 0.009235
#> Pretrain 1.167 1.167 1.422 0.9110 0.005515
#> Individual 1.166 1.166 1.421 0.9115 0.005927
#>
#> Support size:
#>
#> Overall 1
#> Pretrain 1 (0 common + 1 individual)
#> Individual 1
# When we trained our model, we used "lambda.1se" in the first stage of pretraining by default.
# This is a necessary choice to make during model training; we need to select the model
# we want to use to define the offset and penalty factor for the second stage of pretraining.
# We could instead have used "lambda.min":
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "gaussian",
type.measure = "mse", nfolds = 3, overall.lambda = "lambda.min")
# We can use the 'relax' option to fit relaxed lasso models:
fit = ptLasso(x, y, groups = groups, alpha = 0.5,
family = "gaussian", type.measure = "mse",
relax = TRUE)
# As we did for lambda, we may want to specify the choice of gamma for stage one
# of pretraining. (The default is "gamma.1se".)
fit = ptLasso(x, y, groups = groups, alpha = 0.5,
family = "gaussian", type.measure = "mse",
relax = TRUE, overall.gamma = "gamma.min")
# In practice, we may want to try many values of alpha.
# alpha may range from 0 (the overall model with fine tuning) to 1 (the individual models).
# To choose alpha, you may either (1) run ptLasso with different values of alpha
# and measure performance with a validation set, or (2) use cv.ptLasso.
# \donttest{
# Now, we are ready to simulate slightly more realistic data.
# This continuous outcome example has k = 5 groups, where each group has 200 observations.
# There are scommon = 10 features shared across all groups, and
# sindiv = 10 features unique to each group.
# n = 1000 and p = 120 (60 informative features and 60 noise features).
# The coefficients of the common features differ across groups (beta.common).
# In group 1, these coefficients are rep(1, 10); in group 2 they are rep(2, 10), etc.
# Each group has 10 unique features, the coefficients of which are all 3 (beta.indiv).
# The intercept in all groups is 0.
# The variable sigma = 20 indicates that we add noise to y according to 20 * rnorm(n).
set.seed(1234)
k=5
class.sizes=rep(200, k)
scommon=10; sindiv=rep(10, k)
n=sum(class.sizes); p=2*(sum(sindiv) + scommon)
beta.common=3*(1:k); beta.indiv=rep(3, k)
intercepts=rep(0, k)
sigma=20
out = gaussian.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv,
intercepts=intercepts, sigma=20)
x = out$x; y=out$y; groups = out$group
outtest = gaussian.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv,
intercepts=intercepts, sigma=20)
xtest=outtest$x; ytest=outtest$y; groupstest=outtest$groups
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "gaussian", type.measure = "mse")
plot(fit) # to see all of the cv.glmnet models trained
predict(fit, xtest, groupstest) # to predict on new data
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest)
#>
#>
#>
#> alpha = 0.5
#>
#> Support size:
#>
#> Overall 1
#> Pretrain 1 (0 common + 1 individual)
#> Individual 1
predict(fit, xtest, groupstest, ytest=ytest) # if ytest is included, we also measure performance
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean group_1 group_2 r^2
#> Overall 1.162 1.162 1.423 0.9020 0.009235
#> Pretrain 1.167 1.167 1.422 0.9110 0.005515
#> Individual 1.166 1.166 1.421 0.9115 0.005927
#>
#> Support size:
#>
#> Overall 1
#> Pretrain 1 (0 common + 1 individual)
#> Individual 1
# When we trained our model, we used "lambda.1se" in the first stage of pretraining by default.
# This is a necessary choice to make during model training; we need to select the model
# we want to use to define the offset and penalty factor for the second stage of pretraining.
# We could instead have used "lambda.min":
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "gaussian",
type.measure = "mse", nfolds = 3, overall.lambda = "lambda.min")
# We can use the 'relax' option to fit relaxed lasso models:
fit = ptLasso(x, y, groups = groups, alpha = 0.5,
family = "gaussian", type.measure = "mse",
relax = TRUE)
# As we did for lambda, we may want to specify the choice of gamma for stage one
# of pretraining. (The default is "gamma.1se".)
fit = ptLasso(x, y, groups = groups, alpha = 0.5,
family = "gaussian", type.measure = "mse",
relax = TRUE, overall.gamma = "gamma.min")
# In practice, we may want to try many values of alpha.
# alpha may range from 0 (the overall model with fine tuning) to 1 (the individual models).
# To choose alpha, you may either (1) run ptLasso with different values of alpha
# and measure performance with a validation set, or (2) use cv.ptLasso.
# \donttest{
# Now, we are ready to simulate slightly more realistic data.
# This continuous outcome example has k = 5 groups, where each group has 200 observations.
# There are scommon = 10 features shared across all groups, and
# sindiv = 10 features unique to each group.
# n = 1000 and p = 120 (60 informative features and 60 noise features).
# The coefficients of the common features differ across groups (beta.common).
# In group 1, these coefficients are rep(1, 10); in group 2 they are rep(2, 10), etc.
# Each group has 10 unique features, the coefficients of which are all 3 (beta.indiv).
# The intercept in all groups is 0.
# The variable sigma = 20 indicates that we add noise to y according to 20 * rnorm(n).
set.seed(1234)
k=5
class.sizes=rep(200, k)
scommon=10; sindiv=rep(10, k)
n=sum(class.sizes); p=2*(sum(sindiv) + scommon)
beta.common=3*(1:k); beta.indiv=rep(3, k)
intercepts=rep(0, k)
sigma=20
out = gaussian.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv,
intercepts=intercepts, sigma=20)
x = out$x; y=out$y; groups = out$group
outtest = gaussian.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv,
intercepts=intercepts, sigma=20)
xtest=outtest$x; ytest=outtest$y; groupstest=outtest$groups
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "gaussian", type.measure = "mse")
plot(fit) # to see all of the cv.glmnet models trained
 predict(fit, xtest, groupstest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean group_1 group_2 group_3 group_4 group_5 r^2
#> Overall 755.7 755.7 836.0 554.9 565.4 777.9 1044.0 0.5371
#> Pretrain 503.2 503.2 550.6 443.3 553.5 505.6 462.9 0.6918
#> Individual 532.8 532.8 584.1 443.2 567.2 550.5 518.9 0.6736
#>
#> Support size:
#>
#> Overall 64
#> Pretrain 94 (21 common + 73 individual)
#> Individual 109
# }
# \donttest{
# Now, we repeat with a binomial outcome.
# This example has k = 3 groups, where each group has 100 observations.
# There are scommon = 5 features shared across all groups, and
# sindiv = 5 features unique to each group.
# n = 300 and p = 40 (20 informative features and 20 noise features).
# The coefficients of the common features differ across groups (beta.common),
# as do the coefficients specific to each group (beta.indiv).
set.seed(1234)
k=3
class.sizes=rep(100, k)
scommon=5; sindiv=rep(5, k)
n=sum(class.sizes); p=2*(sum(sindiv) + scommon)
beta.common=list(c(-.5, .5, .3, -.9, .1), c(-.3, .9, .1, -.1, .2), c(0.1, .2, -.1, .2, .3))
beta.indiv = lapply(1:k, function(i) 0.9 * beta.common[[i]])
out = binomial.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv)
x = out$x; y=out$y; groups = out$group
outtest = binomial.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv)
xtest=outtest$x; ytest=outtest$y; groupstest=outtest$groups
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "binomial", type.measure = "auc")
plot(fit) # to see all of the cv.glmnet models trained
predict(fit, xtest, groupstest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean group_1 group_2 group_3 group_4 group_5 r^2
#> Overall 755.7 755.7 836.0 554.9 565.4 777.9 1044.0 0.5371
#> Pretrain 503.2 503.2 550.6 443.3 553.5 505.6 462.9 0.6918
#> Individual 532.8 532.8 584.1 443.2 567.2 550.5 518.9 0.6736
#>
#> Support size:
#>
#> Overall 64
#> Pretrain 94 (21 common + 73 individual)
#> Individual 109
# }
# \donttest{
# Now, we repeat with a binomial outcome.
# This example has k = 3 groups, where each group has 100 observations.
# There are scommon = 5 features shared across all groups, and
# sindiv = 5 features unique to each group.
# n = 300 and p = 40 (20 informative features and 20 noise features).
# The coefficients of the common features differ across groups (beta.common),
# as do the coefficients specific to each group (beta.indiv).
set.seed(1234)
k=3
class.sizes=rep(100, k)
scommon=5; sindiv=rep(5, k)
n=sum(class.sizes); p=2*(sum(sindiv) + scommon)
beta.common=list(c(-.5, .5, .3, -.9, .1), c(-.3, .9, .1, -.1, .2), c(0.1, .2, -.1, .2, .3))
beta.indiv = lapply(1:k, function(i) 0.9 * beta.common[[i]])
out = binomial.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv)
x = out$x; y=out$y; groups = out$group
outtest = binomial.example.data(k=k, class.sizes=class.sizes,
scommon=scommon, sindiv=sindiv,
n=n, p=p,
beta.common=beta.common, beta.indiv=beta.indiv)
xtest=outtest$x; ytest=outtest$y; groupstest=outtest$groups
fit = ptLasso(x, y, groups = groups, alpha = 0.5, family = "binomial", type.measure = "auc")
plot(fit) # to see all of the cv.glmnet models trained
 predict(fit, xtest, groupstest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> allGroups mean wtdMean group_1 group_2 group_3
#> Overall 0.5990 0.5963 0.5963 0.6006 0.6772 0.5112
#> Pretrain 0.6442 0.6631 0.6631 0.6965 0.7752 0.5177
#> Individual 0.6429 0.6580 0.6580 0.6948 0.7607 0.5186
#>
#> Support size:
#>
#> Overall 8
#> Pretrain 40 (3 common + 37 individual)
#> Individual 40
# }
if (FALSE) { # \dontrun{
### Model fitting with parallel = TRUE
require(doMC)
registerDoMC(cores = 4)
fit = ptLasso(x, y, groups = groups, family = "gaussian", type.measure = "mse", parallel=TRUE)
} # }
# \donttest{
# Multiresponse pretraining:
# Now let's consider the case of a multiresponse outcome. We'll start by simulating data:
set.seed(1234)
n = 1000; ntrain = 500;
p = 500
sigma = 2
x = matrix(rnorm(n*p), n, p)
beta1 = c(rep(1, 5), rep(0.5, 5), rep(0, p - 10))
beta2 = c(rep(1, 5), rep(0, 5), rep(0.5, 5), rep(0, p - 15))
mu = cbind(x %*% beta1, x %*% beta2)
y = cbind(mu[, 1] + sigma * rnorm(n),
mu[, 2] + sigma * rnorm(n))
cat("SNR for the two tasks:", round(diag(var(mu)/var(y-mu)), 2), fill=TRUE)
#> SNR for the two tasks: 1.6 1.44
cat("Correlation between two tasks:", cor(y[, 1], y[, 2]), fill=TRUE)
#> Correlation between two tasks: 0.5164748
xtest = x[-(1:ntrain), ]
ytest = y[-(1:ntrain), ]
x = x[1:ntrain, ]
y = y[1:ntrain, ]
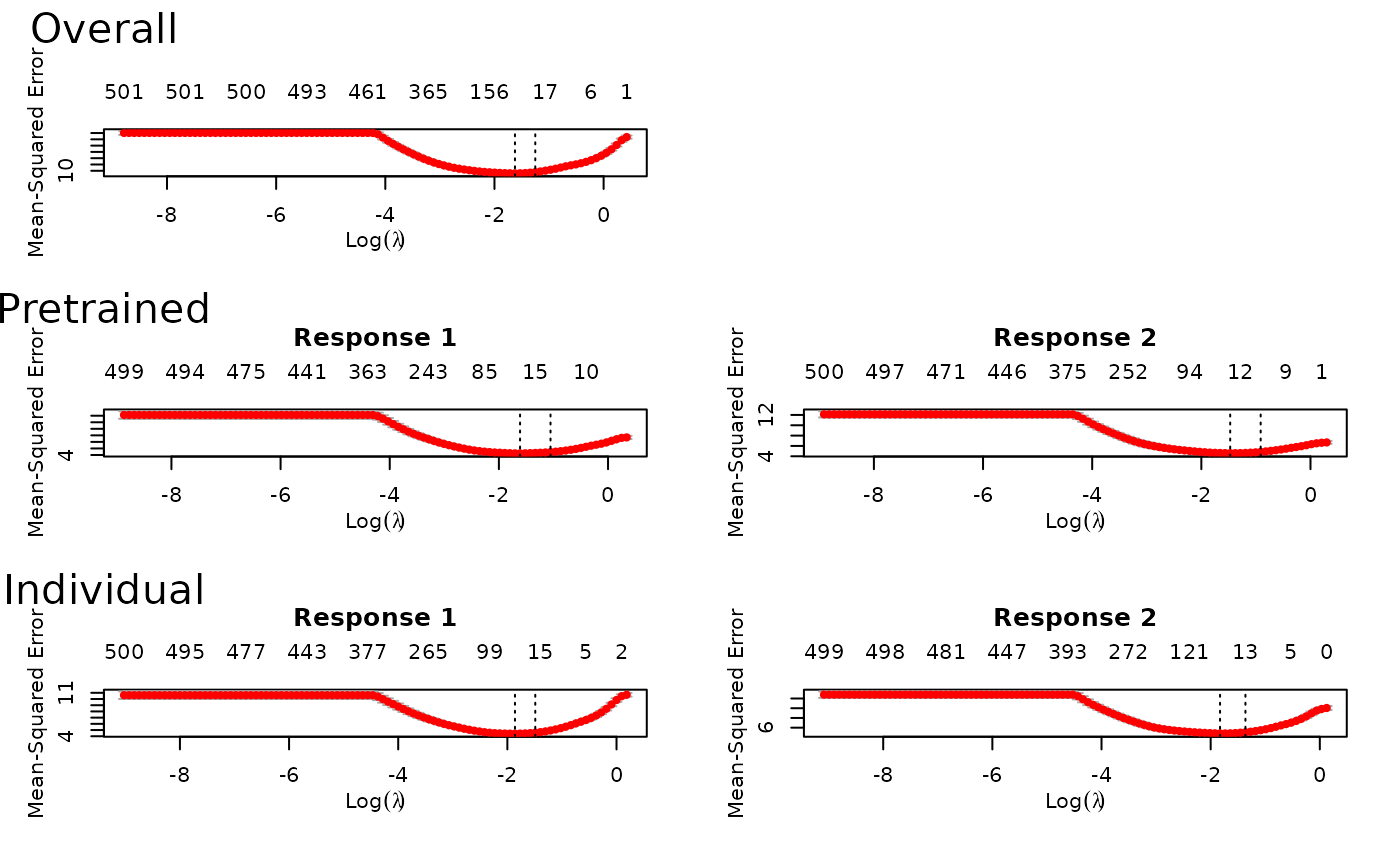
fit = ptLasso(x, y, type.measure = "mse", use.case = "multiresponse")
plot(fit) # to see all of the cv.glmnet models trained
predict(fit, xtest, groupstest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, groupstest = groupstest,
#> ytest = ytest)
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> allGroups mean wtdMean group_1 group_2 group_3
#> Overall 0.5990 0.5963 0.5963 0.6006 0.6772 0.5112
#> Pretrain 0.6442 0.6631 0.6631 0.6965 0.7752 0.5177
#> Individual 0.6429 0.6580 0.6580 0.6948 0.7607 0.5186
#>
#> Support size:
#>
#> Overall 8
#> Pretrain 40 (3 common + 37 individual)
#> Individual 40
# }
if (FALSE) { # \dontrun{
### Model fitting with parallel = TRUE
require(doMC)
registerDoMC(cores = 4)
fit = ptLasso(x, y, groups = groups, family = "gaussian", type.measure = "mse", parallel=TRUE)
} # }
# \donttest{
# Multiresponse pretraining:
# Now let's consider the case of a multiresponse outcome. We'll start by simulating data:
set.seed(1234)
n = 1000; ntrain = 500;
p = 500
sigma = 2
x = matrix(rnorm(n*p), n, p)
beta1 = c(rep(1, 5), rep(0.5, 5), rep(0, p - 10))
beta2 = c(rep(1, 5), rep(0, 5), rep(0.5, 5), rep(0, p - 15))
mu = cbind(x %*% beta1, x %*% beta2)
y = cbind(mu[, 1] + sigma * rnorm(n),
mu[, 2] + sigma * rnorm(n))
cat("SNR for the two tasks:", round(diag(var(mu)/var(y-mu)), 2), fill=TRUE)
#> SNR for the two tasks: 1.6 1.44
cat("Correlation between two tasks:", cor(y[, 1], y[, 2]), fill=TRUE)
#> Correlation between two tasks: 0.5164748
xtest = x[-(1:ntrain), ]
ytest = y[-(1:ntrain), ]
x = x[1:ntrain, ]
y = y[1:ntrain, ]
fit = ptLasso(x, y, type.measure = "mse", use.case = "multiresponse")
plot(fit) # to see all of the cv.glmnet models trained
 predict(fit, xtest) # to predict with new data
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest)
#>
#>
#> alpha = 0.5
#>
#> Support size:
#>
#> Overall 57
#> Pretrain 29 (19 common + 10 individual)
#> Individual 80
predict(fit, xtest, ytest=ytest) # if ytest is included, we also measure performance
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean response_1 response_2
#> Overall 9.394 4.697 4.227 5.168
#> Pretrain 9.022 4.511 4.144 4.878
#> Individual 9.465 4.733 4.243 5.222
#>
#> Support size:
#>
#> Overall 57
#> Pretrain 29 (19 common + 10 individual)
#> Individual 80
# By default, we used lambda = "lambda.min" to measure performance.
# We could instead use lambda = "lambda.1se":
predict(fit, xtest, ytest=ytest, s="lambda.1se")
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest, s = "lambda.1se")
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean response_1 response_2
#> Overall 9.879 4.940 4.387 5.492
#> Pretrain 9.481 4.740 4.210 5.271
#> Individual 9.965 4.983 4.341 5.624
#>
#> Support size:
#>
#> Overall 19
#> Pretrain 19 (19 common + 0 individual)
#> Individual 27
# We could also use the glmnet option relax = TRUE:
fit = ptLasso(x, y, type.measure = "mse", relax = TRUE, use.case = "multiresponse")
# }
# \donttest{
# Time series pretraining
# Now suppose we have time series data with a binomial outcome measured at 3 different time points.
set.seed(1234)
n = 600; ntrain = 300; p = 50
x = matrix(rnorm(n*p), n, p)
beta1 = c(rep(0.5, 10), rep(0, p-10))
beta2 = beta1 + c(rep(0, 10), runif(5, min = 0, max = 0.5), rep(0, p-15))
beta3 = beta1 + c(rep(0, 10), runif(5, min = 0, max = 0.5), rep(.5, 5), rep(0, p-20))
y1 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta1)))
y2 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta2)))
y3 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta3)))
y = cbind(y1, y2, y3)
xtest = x[-(1:ntrain), ]
ytest = y[-(1:ntrain), ]
x = x[1:ntrain, ]
y = y[1:ntrain, ]
fit = ptLasso(x, y, use.case="timeSeries", family="binomial", type.measure = "auc")
plot(fit)
predict(fit, xtest) # to predict with new data
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest)
#>
#>
#> alpha = 0.5
#>
#> Support size:
#>
#> Overall 57
#> Pretrain 29 (19 common + 10 individual)
#> Individual 80
predict(fit, xtest, ytest=ytest) # if ytest is included, we also measure performance
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean response_1 response_2
#> Overall 9.394 4.697 4.227 5.168
#> Pretrain 9.022 4.511 4.144 4.878
#> Individual 9.465 4.733 4.243 5.222
#>
#> Support size:
#>
#> Overall 57
#> Pretrain 29 (19 common + 10 individual)
#> Individual 80
# By default, we used lambda = "lambda.min" to measure performance.
# We could instead use lambda = "lambda.1se":
predict(fit, xtest, ytest=ytest, s="lambda.1se")
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest, s = "lambda.1se")
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (Mean squared error):
#>
#> allGroups mean response_1 response_2
#> Overall 9.879 4.940 4.387 5.492
#> Pretrain 9.481 4.740 4.210 5.271
#> Individual 9.965 4.983 4.341 5.624
#>
#> Support size:
#>
#> Overall 19
#> Pretrain 19 (19 common + 0 individual)
#> Individual 27
# We could also use the glmnet option relax = TRUE:
fit = ptLasso(x, y, type.measure = "mse", relax = TRUE, use.case = "multiresponse")
# }
# \donttest{
# Time series pretraining
# Now suppose we have time series data with a binomial outcome measured at 3 different time points.
set.seed(1234)
n = 600; ntrain = 300; p = 50
x = matrix(rnorm(n*p), n, p)
beta1 = c(rep(0.5, 10), rep(0, p-10))
beta2 = beta1 + c(rep(0, 10), runif(5, min = 0, max = 0.5), rep(0, p-15))
beta3 = beta1 + c(rep(0, 10), runif(5, min = 0, max = 0.5), rep(.5, 5), rep(0, p-20))
y1 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta1)))
y2 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta2)))
y3 = rbinom(n, 1, prob = 1/(1 + exp(-x %*% beta3)))
y = cbind(y1, y2, y3)
xtest = x[-(1:ntrain), ]
ytest = y[-(1:ntrain), ]
x = x[1:ntrain, ]
y = y[1:ntrain, ]
fit = ptLasso(x, y, use.case="timeSeries", family="binomial", type.measure = "auc")
plot(fit)
 predict(fit, xtest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> mean response_1 response_2 response_3
#> Pretrain 0.8194 0.8194 0.8035 0.8354
#> Individual 0.7997 0.8194 0.7691 0.8106
#>
#> Support size:
#>
#> Pretrain 43 (26 common + 17 individual)
#> Individual 47
# The glmnet option relax = TRUE:
fit = ptLasso(x, y, type.measure = "auc", family = "binomial", relax = TRUE,
use.case = "timeSeries")
plot(fit)
predict(fit, xtest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> mean response_1 response_2 response_3
#> Pretrain 0.8194 0.8194 0.8035 0.8354
#> Individual 0.7997 0.8194 0.7691 0.8106
#>
#> Support size:
#>
#> Pretrain 43 (26 common + 17 individual)
#> Individual 47
# The glmnet option relax = TRUE:
fit = ptLasso(x, y, type.measure = "auc", family = "binomial", relax = TRUE,
use.case = "timeSeries")
plot(fit)
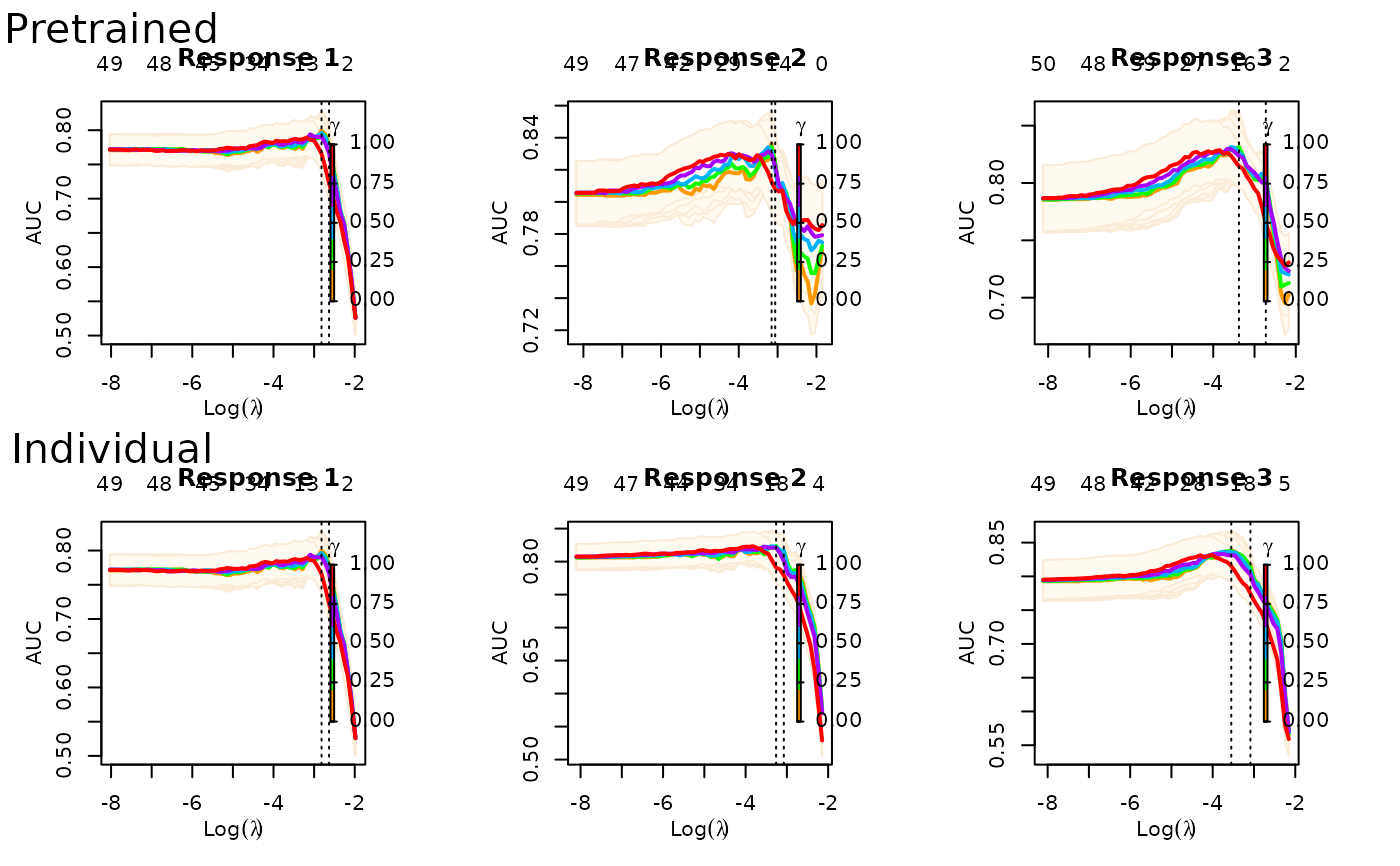 predict(fit, xtest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> mean response_1 response_2 response_3
#> Pretrain 0.8123 0.8298 0.7818 0.8252
#> Individual 0.8018 0.8298 0.7647 0.8110
#>
#> Support size:
#>
#> Pretrain 26 (12 common + 14 individual)
#> Individual 29
# }
predict(fit, xtest, ytest=ytest)
#>
#> Call:
#> predict.ptLasso(object = fit, xtest = xtest, ytest = ytest)
#>
#>
#>
#> alpha = 0.5
#>
#> Performance (AUC):
#>
#> mean response_1 response_2 response_3
#> Pretrain 0.8123 0.8298 0.7818 0.8252
#> Individual 0.8018 0.8298 0.7647 0.8110
#>
#> Support size:
#>
#> Pretrain 26 (12 common + 14 individual)
#> Individual 29
# }